What are the key concepts and principles in game theory that are most essential for strategic analysis?

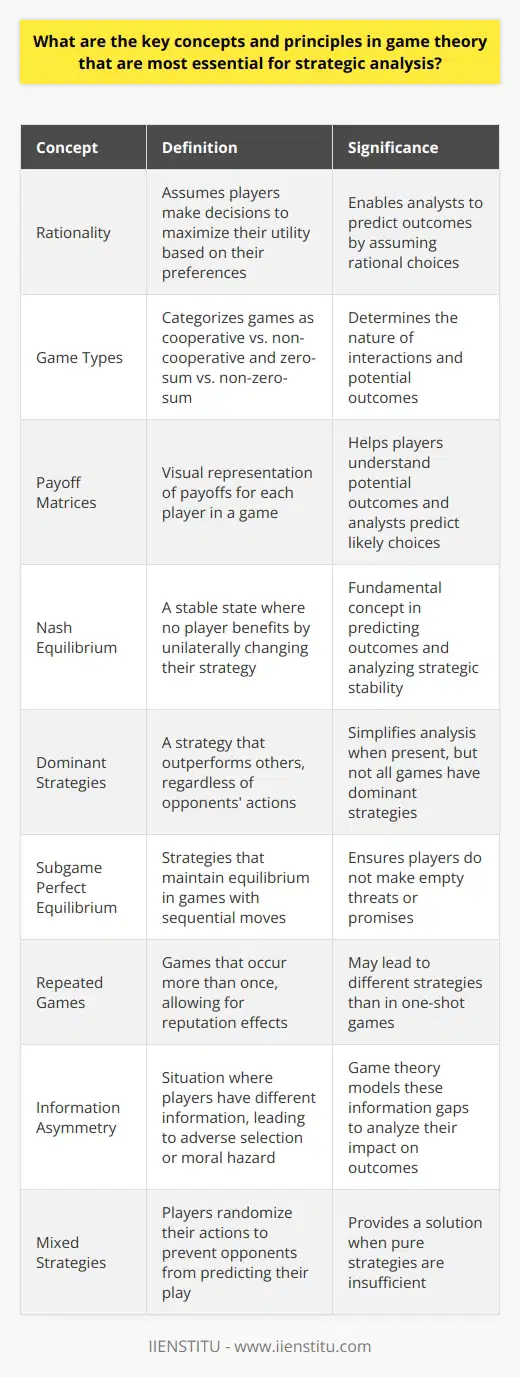
<h3>Game Theory Fundamentals</h3><p>Game theory offers a framework for understanding strategic interactions. It bridges economics, political science, and psychology. Strategic analysis heavily relies on several key concepts. Each principle plays a pivotal role in analyzing competitive and cooperative settings.</p><h4>Rationality</h4><p>At its core, game theory assumes rational agents. Players aim for the best outcome, given their preferences. They make decisions to maximize utility. Analysts predict outcomes by assuming rational choices.</p><h4>Game Types</h4><p>Games fall into different categories. These include cooperative vs. non-cooperative and zero-sum vs. non-zero-sum. Cooperative games involve binding agreements. Non-cooperative games do not. Zero-sum games have fixed winnings. Non-zero-sum games allow mutual gains or losses.</p><h4>Payoff Matrices</h4><p>The payoff matrix is a visual representation. It shows the payoffs for each player. Matrices help players understand potential outcomes. Analysts use them to predict likely choices.</p><h4>Nash Equilibrium</h4><p>A Nash Equilibrium occurs when no player benefits by changing their strategy. It reflects stability in the game. Each player's strategy is optimal, given the others'. It's a fundamental concept in predicting outcomes.</p><h4>Dominant Strategies</h4><p>A dominant strategy outperforms others, regardless of opponents' actions. If it exists, it simplifies analysis. Not all games have dominant strategies.</p><h4>Subgame Perfect Equilibrium</h4><p>This refers to strategies that maintain equilibrium. It's relevant in games with sequential moves. It ensures players do not make empty threats or promises.</p><h4>Repeated Games</h4><p>Some games occur more than once. These are repeated games. They allow for reputation effects. They may lead to different strategies than in one-shot games.</p><h4>Information Assymetry</h4><p>This occurs when players have different information. It can lead to adverse selection or moral hazard. Games model these information gaps.</p><h4>Mixed Strategies</h4><p>Pure strategies may not always suffice. Players sometimes randomize their actions. They use mixed strategies to do so. This can prevent opponents from predicting their play.</p><p>Game theory brings clarity to strategic decisions. The concepts mentioned above are building blocks. Together, they form a solid foundation for strategic analysis. Understanding these principles is crucial for making informed decisions in any game-theoretic context.</p>

How does game theory inform decision-making processes in the context of practical applications?

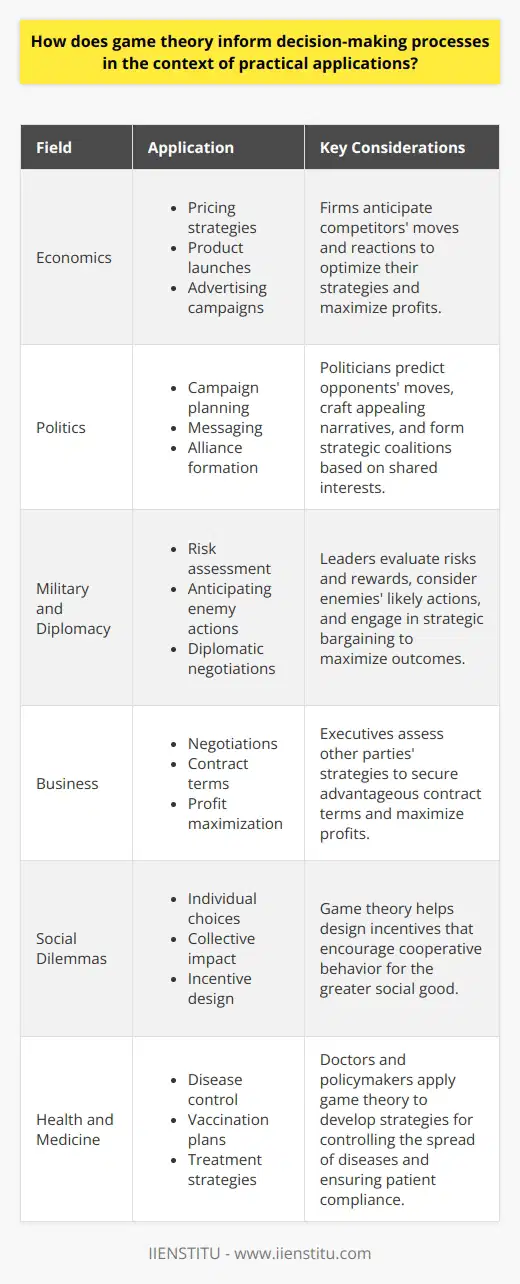
<h3>Understanding Game Theory</h3><p><strong>Game theory</strong> explores strategic interaction. It applies to economics, politics, and more. Scholars and practitioners heavily rely on it. It informs various decision-making processes.</p><h4>Decision-Making in Economics</h4><p>In economics, game theory deals with market strategies. Firms consider competitors' potential moves. They anticipate reactions and strategize accordingly. This process influences pricing, product launches, and advertising campaigns. </p><p>- <strong>Pricing</strong>: Firms set optimal prices.</p><p>- <strong>Product launches</strong>: Timing and features reflect competition.</p><p>- <strong>Advertising</strong>: Firms counter competitors' campaigns.</p><h4>Political Strategy and Elections</h4><p>Politicians use game theory to plan campaigns. They predict opponents' moves. They tailor messages to sway swing voters. Alliances form based on shared interests.</p><p>- <strong>Predicting moves</strong>: Parties analyze rivals' plans.</p><p>- <strong>Messaging</strong>: Politicians craft appealing narratives.</p><p>- <strong>Forming alliances</strong>: Coalitions emerge strategically.</p><h4>Military Tactics and Diplomacy</h4><p>Game theory guides military decisions. Leaders evaluate risks and rewards. They consider enemies' likely actions. Diplomacy involves similar calculations.</p><p>- <strong>Risk assessment</strong>: Commanders weigh potential losses.</p><p>- <strong>Enemy actions</strong>: Moves are anticipated.</p><p>- <strong>Diplomatic negotiations</strong>: Countries bargain, predict outcomes.</p><h4>Business Negotiations and Contracts</h4><p>Executives negotiate using game theory. They assess other parties' strategies. This ensures advantageous contract terms. Profit maximization is the goal.</p><p>- <strong>Strategy assessment</strong>: Executives predict others' terms.</p><p>- <strong>Advantageous terms</strong>: Negotiations aim for the best deal.</p><p>- <strong>Profit maximization</strong>: The ultimate objective.</p><h4>Solving Social Dilemmas</h4><p>Social dilemmas involve group interaction. Individuals make choices impacting the collective. Game theory helps design incentives for social good.</p><p>- <strong>Individual choices</strong>: Personal decisions affect groups.</p><p>- <strong>Collective impact</strong>: Outcomes have broader effects.</p><p>- <strong>Designing incentives</strong>: Strategies encourage cooperative behavior.</p><h4>Health and Medicine</h4><p>Doctors and policymakers apply game theory in health. They strategize to control diseases. Vaccination and treatment plans are game-theoretic strategies.</p><p>- <strong>Disease control</strong>: Strategies limit spread.</p><p>- <strong>Vaccination plans</strong>: Approaches aim for herd immunity.</p><p>- <strong>Treatment plans</strong>: Patient compliance is critical.</p><h3>Game Theory's Practical Impact</h3><p><strong>Game theory</strong> evolves as a crucial tool. It offers structured frameworks for choices. Decision-makers better forecast outcomes using it. It enhances strategic planning across fields. Game theory informs smarter, forward-thinking decisions.</p>

Can you provide any examples where game theory has been successfully applied to resolve real-world, strategic dilemmas?

<h3>Game Theory in Real-world Strategic Dilemmas</h3><p>Game theory stands as an essential part of modern strategy. This theory finds utility in diverse areas — economics, politics, psychology, and more. Experts often turn to game theory to clarify strategic interactions among rational actors. These actors could be individuals, businesses, or nations. Analyzing their choices leads to insights about cooperation and conflict. Several real-world examples show how game theory has proved effective. Below are a few domains where game theory has shone.</p><h4>Economics and Business</h4><p>In economics, firms use game theory for pricing strategies. They consider rival pricing before setting their own. This behavior follows the Cournot Competition model. Firms decide on quantities to produce, knowing rivals will respond similarly. Pricing and output choices reflect understanding of this strategic interdependence.</p><p>Auction design serves as another strong example. Game theory helps craft auctions to maximize seller profit. The well-known 1994 FCC spectrum auction demonstrates this well. The government used game theoretic insights to sell radio frequencies. This method ensured efficient use and maximized revenue.</p><p>Corporate takeovers also involve game theory. Companies strategize to manage hostile takeovers. They play a game predicting rival maneuvers. Then they prepare defenses or counteroffers. The "poison pill" strategy is a direct outcome of such game-theoretic planning.</p><h4>International Relations</h4><p>Game theory applies to international relations, especially in conflict resolution. The Cuban Missile Crisis is a classic case. Both the US and the Soviet Union had to contemplate each other's potential moves. They understood the grave consequences of escalation. This mutual understanding helped to avoid a nuclear standoff.</p><p>Trade negotiations also use game theory principles. Nations negotiate tariffs and trade deals, ensuring mutual gain while protecting home industries. Game theory helps parties understand the benefits of cooperation over protectionism.</p><h4>Environmental Policy</h4><p>Environmental agreements incorporate game theory. Nations face the temptation to free-ride on others' conservation efforts. Game theory models, such as the Tragedy of the Commons, guide policymakers. This model aids in designing better incentive systems for pollution control.</p><p>Negotiations on climate change involve game theory too. The Paris Agreement is an instance where countries tackled the free-rider problem. They committed to individual but cooperative action to reduce emissions.</p><h4>Technology and Cybersecurity</h4><p>Tech companies design networks with game theory principles. They prepare for potential breaches by considering how hackers might strike. Then they bolster defenses accordingly. This proactive approach reduces system vulnerabilities.</p><p>In cybersecurity, defense strategies become a game against attackers. Defenders make moves to protect data. Attackers respond with new hacking techniques. This ongoing interaction defines the state of cybersecurity.</p><p>The diverse applications of game theory offer a glimpse into its power. In each case, strategic decision-making becomes clearer. Leaders rely on game theory to seek optimal solutions to complex problems. The examples provided affirm its value in addressing strategic dilemmas. Game theory's influence stretches across domains, showing its universal relevance.</p>

Game Theory: Strategic Analysis and Practical Applications

Game Theory, an essential framework in economics and strategic studies, offers insight into the complex realm of human decision-making. By examining the interactions among rational players within competitive and cooperative environments, Game Theory provides a structured approach to predicting and influencing outcomes in various scenarios. This article delves into the intricate principles of Game Theory, exploring its practical applications in decision-making, economics, the burgeoning technology and AI industries, as well as addressing the challenges and criticisms it faces. Whether applied to everyday life decisions or complex market behaviors, Game Theory remains a powerful tool for strategic analysis and problem-solving.

In doing so, we will shed light on not just the theory itself but also on how one can deepen their understanding through structured learning opportunities like an online certificate course or a comprehensive problem solving certification.

The Principles of Game Theory

The underpinning concepts of Game Theory are integral to understanding strategic interactions. At its core, this mathematical model assumes rational players who are looking to maximize their personal payoffs, whether that entails cooperation or competition. The theory divides games into various categories such as cooperative or non-cooperative, symmetric or asymmetric, and zero-sum or non-zero-sum, each describing different strategic situations the players may face.

Assumptions in Game Theory are the bedrock of its predictive capabilities. Participants are commonly presumed to be rational, seeking to maximize their utility. They have perfect knowledge of the payoff matrix structure, albeit not necessarily of the actions other players will take. Furthermore, the number of players, available strategies, and potential outcomes are known. Although these assumptions are idealized versions of reality, they create a simplified framework to analyze complex interactions.

Illustrations through real-life examples make the abstract principles of Game Theory far more tangible. Markets operate under the premise of competition, where companies must anticipate competitors' actions. Political campaigns are strategic in nature, as candidates aim to win voters under the assumption of rational choice. These parallels between theoretical concepts and real-world scenarios validate Game Theory's extensive applicability and facilitate the understanding of its core principles.

Game Theory in Decision Making

In the realm of decision making, Game Theory serves as a vital tool for analyzing strategic interactions in various sectors, from business negotiations to political strategy. It allows individuals and organizations to anticipate the moves of others and respond in a way that will most likely result in a favorable outcome. This strategic anticipation involves identifying best responses, potential retaliations, and aligning actions to align with desired objectives.

Understanding dominant strategies is a key facet of utilizing Game Theory effectively. A dominant strategy occurs when one particular strategy results in preferable outcomes for a player, irrespective of the other players' actions. Identifying these strategies can greatly simplify the decision-making process and is especially vital in competitive environments where the margin for error is remarkably thin.

Understanding Nash equilibrium

Nash Equilibrium, named after mathematician John Nash, is another fundamental concept in Game Theory. It is a state within a game where no player can benefit by changing their strategy while the other players keep theirs unchanged. This concept is paramount as it often predicts the outcome of strategic interactions, providing a stable solution where individuals or firms make decisions considering the likely responses of others.

Real-world decision-making scenarios are replete with examples of Game Theory at play. Corporate decisions on pricing, product launches, and market entries often hinge upon anticipating competitors' moves and formulating counter-strategies. International relations and diplomatic strategies are grounded in Game Theory, with governments analyzing potential responses before making critical decisions on alliances, treaties, and conflicts.

Economical Aspect of Game Theory

Game Theory holds an influential position in economics by providing a structured approach to understanding and predicting individual and collective behaviors within markets. It serves as a cornerstone of microeconomic theory, which deals with the actions of individuals and firms, and has extensive implications for market dynamics and economic policy design.

Market competition is an area where Game Theory's principles are vividly applied. Firms engage in strategic moves, such as price setting, creating barriers to entry, or forming alliances, each of which can be modeled and studied through the lens of Game Theory. Analyzing these competitive environments helps businesses optimize their strategies for better market positioning and profitability.

Market negotiation

Market negotiations, too, serve as a fine illustration of Game Theory's applicability. Whether in mergers and acquisitions, contract negotiations or resolving trade disputes, the theory guides participants in making strategic offers and counteroffers. The anticipation of the other party's moves, preferences, and possible outcomes greatly influences the tactics and final agreements.

Illustrations in the economic field are not short in supply. The OPEC oil pricing negotiations are a testament to Game Theory, where each member country must consider the actions and reactions of others when deciding on production levels. Similarly, auction designs for selling government securities or privatizing public assets are deeply rooted in Game Theory principles. These examples embody the theory's power to model and shape economic behaviors.

Game Theory in the Technology and AI Industry

The role of Game Theory in the technology and AI sector is rapidly expanding. As systems become more interconnected and autonomous, creating effective algorithms that can anticipate and adapt to other agents' behaviors becomes crucial. This has profound implications for the design of software, as well as the strategic decisions made by tech companies.

Game Theory is intricately woven into the development of AI and machine learning algorithms. As AI systems interact with one another and with humans, they must make decisions that align with optimizing their set objectives, a process that Game Theory models proficiently. Whether in autonomous vehicles, financial trading algorithms, or content recommendation engines, these strategies play a pivotal role.

Real-life examples bolster our understanding of Game Theory's role in AI. Autonomous vehicles, for instance, must predict the actions of human drivers and other autonomous systems to navigate safely and efficiently. In e-commerce, recommendation algorithms use Game Theory principles to optimize their suggestions based on user interactions and competitive dynamics within the marketplace. These instances highlight the seamless integration of Game Theory in the technology and AI sectors.

Challenges and Criticisms of Game Theory

Despite its widespread application, Game Theory is not without its limitations and challenges. One of the primary concerns is that the theory relies heavily on the assumption of rational behavior, which does not always align with actual human decision-making that can be influenced by biases, emotions, and imperfect information.

Criticism of Game Theory often revolves around its sometimes oversimplified model of human behavior and the potential detachment from real-world complexity. Critics argue that the assumptions of complete information and rational action are rarely met, questioning the practical relevance of its predictions and solutions.

In defense of these criticisms, scholars and practitioners highlight that Game Theory provides a foundational framework from which more complex and nuanced models might be developed. Admitting that no model can perfectly encapsulate human behavior, proponents underline that Game Theory excels as a starting point for understanding strategic interactions, one that can be iteratively refined to better reflect real-world complexities.

Throughout this exploration, the versatility and significance of Game Theory in analyzing and informing strategic decisions have been apparent. Its principles shed light on the intricacies of human and organizational behavior, offering a lens through which competitive and cooperative activities can be understood and optimized. The value of structured learning in the form of an online certificate course in Game Theory should not be underestimated, as it offers individuals the comprehensive knowledge and expert approach required to apply these concepts effectively.

In sum, Game Theory presents a robust set of tools that continue to influence not only academic thought but practical decision-making across various sectors. As we look to the future, ongoing advancements in AI, machine learning, and the digital economy will likely bring Game Theory into even greater prominence, suggesting its continued evolution and application in increasingly sophisticated ways.