In the intricate tapestry of decision-making, probability analysis emerges as a pivotal thread, interlacing the fabric of logic and uncertainty into coherent patterns of judgment. This article delves into the realm of probability analysis, a domain that has etched its significance across various fields, catalyzing our understanding of risk, chance, and decision-making. Probability analysis is the compelling cogs in the clockwork of predictability, a mechanism that we harness to peer through the haziness of stochastic events and make informed decisions.
Through a lucid exploration of its theoretical underpinnings and practical applications, we shall unravel the enigma of probability analysis, illustrating its potency in shaping the contours of enlightened choice-making.
Introduction to Probability Analysis
Definition and significance of probability analysis: Probability analysis is the study and interpretation of the likelihood of occurrences within a specific context, wherein outcomes are uncertain. This mathematical framework is integral to a multitude of disciplines, providing an evidential basis for predictions and an underpinning for strategic decisions. Its application spans numerous sectors, from gauging the volatility of financial markets to the probabilities underlying quantum physics phenomena. At its core, probability analysis quantifies intuition, endowing it with numerical precision and allowing for a systematic approach to uncertainty.
Brief history and application of probability analysis in different fields: The germination of probability analysis dates back centuries, with early conceptions emerging from the study of games of chance. Over time, luminaries like Blaise Pascal and Pierre-Simon Laplace nurtured its philosophical and mathematical structures, culminating in a robust academic discipline. Today, its tentacles reach into the realms of meteorology, medicine, sports, and even jurisprudence, where it aids forensic analysis. Its versatility offers a prism through which we can learn problem solving with finesse, underscoring the randomness that permeates our very existence.
Theoretical Framework of Probability
Explanation of key probability concepts: Probability theory is constructed on several key concepts that provide a scaffold for understanding randomness. A 'random experiment' denotes a process that yields various outcomes without a predictable certainty. Each 'outcome' is a potential result of an experiment, while an 'event' encapsulates a set of outcomes of interest. The 'sample space' represents the totality of all possible outcomes, and a 'probability measure' assigns a numerical value to the likelihood of events, conforming to a set of prescribed axioms.
Major theories in probability: To grasp the essence of probability, it is crucial to acquaint oneself with its three foundational theories. The 'classical theory' presupposes equally likely outcomes, furnishing a theoretical estimate of probabilities. The 'empirical theory' relies on the frequency of events in long runs of observations, aligning closely with the law of large numbers. Lastly, the 'axiomatic theory' founded by Kolmogorov, operates on a set of axioms that establish probability as a mathematical discipline, independent of physical interpretation.
Description of probability properties: Probability adheres to intrinsic properties that maintain its mathematical coherence. 'Non-negativity' ensures that probabilities are not less than zero, reflecting the impossibility of negative likelihoods. 'Normalization' mandates that the probability of the entire sample space is unity, encapsulating certainty. 'Additivity', also known as the 'additive rule', postulates that the probability of collective exclusive events equals the sum of their individual probabilities.
Methods of Conducting Probability Analysis
Probability tree diagrams: The probability tree diagram is an illustrative tool that maps the possible outcomes of sequential events and their associated probabilities. Its utility lies in its ability to decompose complex processes into accessible, bifurcating pathways. Constructing these diagrams entails a chronological representation, with branches denoting outcomes and nodes signifying decision points. This visual heuristic aids in clarifying otherwise convoluted scenarios, offering a scaffold upon which to learn problem solving strategies.
Probability distribution: Central to probability analysis is the concept of a probability distribution, which chronicles the likelihood of outcomes across a spectrum. Discrete probability distributions cater to countable outcomes, such as the roll of dice, while continuous probability distributions deal with uncountably infinite possibilities, such as measurements of weight or time. This division encapsulates the dichotomy within the probabilistic landscape, each with distinct functions and characteristics.
Conditional Probability and Bayes' Theorem: Unveiling the conditions under which certain events occur, conditional probability plays a pivotal role in refining our predictive capabilities. Bayes' theorem, a cornerstone of probabilistic logic, leverages prior knowledge to update beliefs in light of new evidence. This reciprocal dance between hypothesis and data forms the bedrock of statistical inference, enabling astute recalibration of predictions as additional information becomes available.
Application of Probability Analysis
Application in Engineering: Within the engineering sphere, probability analysis dictates design, resilience, and optimization. Engineers deploy probabilistic models to predict the performance of structures under diverse conditions, mitigating risks linked to material failure or unpredictable loads. This theoretical rigor translates into safer buildings, more reliable systems, and extends the frontier of engineering possibilities.
Application in Business and Economics: In the business and economic domains, probability analysis serves as a compass, guiding investment decisions and market predictions. It illuminates the murky waters of financial risks and returns, enabling practitioners to navigate through the volatile currents of economic uncertainty. Through nuanced assessments of probabilistic outcomes, businesses optimize their strategies, propelling economic engines with insightful deliberation.
Application in Data Science: The ascendancy of data science has amplified the demand for robust probability models, crucial for extracting meaningful insights from vast troves of data. Predictive analytics, machine learning algorithms, and big data processing are predicated on principled probabilistic reasoning, which carves out patterns and predictions from the raw clay of data. As a result, data science, arm-in-arm with probability analysis, spawns profound advancements in how we comprehend and leverage information.
Conclusion
Probability analysis thus plays a quintessential role in demystifying the uncertainties intrinsic to a plethora of domains, serving as a beacon of clarity in a sea of stochastic influences. The principles and methods of probability analysis punctuate the human quest for rationality in the face of chance, guiding us in our quest for knowledge and sound decision-making. As we depart from this exposition, there rests an impetus upon us to further infuse the insights of probability analysis into our fields of interest, spurning deeper exploration and understanding.
Further Reading and Resources
Those who seek to deepen their immersion in the profound depths of probability analysis may find solace in the vast selection of advanced study materials and textbooks available. For those drawn to the digital age, online certificate courses proffer structured learning pathways, bristling with the convenience and accessibility that modern technology affords. A diligent pursuit of these educational channels shall undoubtedly enrich and elevate one's analytical acumen, engendering a new legion of probabilistic thinkers ready to confront the unfathomable complexities of the world.
Frequently Asked Questions
What are the key principles and methodologies in probability analysis used for effective decision-making?
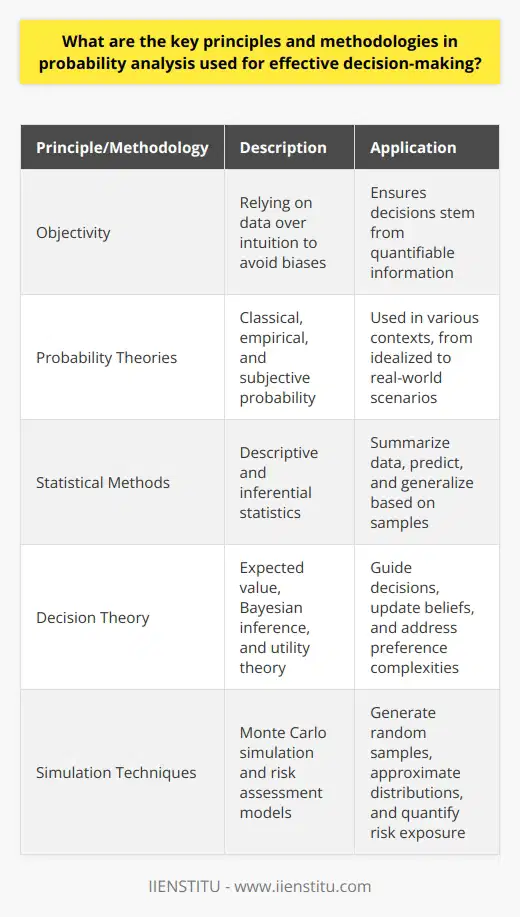
Probability analysis stands at the crux of modern decision-making. It involves complex and dynamic systems that require precise approaches. Experts in the field rely on several key principles and methodologies. Understanding these concepts helps steer effective strategies in uncertain environments.
Core Principles of Probability Analysis
Objectivity
Objectivity grounds all statistical reasoning. Analysts must rely on data over intuition to avoid biases. This principle ensures decisions stem from quantifiable information.
Comprehensiveness
A comprehensive view captures all relevant elements. Decision-makers consider various risk factors and outcomes to minimize oversights.
Repeatability
Repeatability in analysis signifies reliability. Methods must yield consistent results across multiple tests. This consistency builds confidence in the derived probabilities.
Rationality
Rational actors use probability to guide choices. They weigh potential gains against losses. Maximizing expected utility is often the end goal.
Continual Revision
Analysts should update probabilities with new data. This flexibility allows for adjustments when facing novel information. Continual revision keeps analyses relevant over time.
Methodologies in Probability Analysis
Probability Theories
Classical probability deals with equal-likelihood events. It is common in idealized contexts. Think of a fair coin toss.
Empirical probability emerges from historical data. It reflects observed frequencies. Its use prevails in real-world scenarios.
Subjective probability is belief-based. It uses expert judgment when data lacks. Its application is widespread in industries like finance and insurance.
Statistical Methods
Descriptive statistics summarize data through measures like mean and variance. These indicators provide insight into historical performance.
Inferential statistics extend beyond data at hand. They predict and generalize based on samples. Confidence intervals and hypothesis tests fall under this category.
Decision Theory
Expected value calculations forecast long-term averages. They guide decisions where outcomes have known probabilities.
Bayesian inference updates beliefs with evidence. It combines prior knowledge with new data. This approach adjusts probabilities to reflect current understanding.
Utility theory addresses preference complexities. Not all decisions are about maximizing monetary value. Utility measures satisfaction or subjective value.
Simulation Techniques
Monte Carlo simulation generates many random samples. Analysts use these to approximate complex distributions. It offers insight into potential variability and outcomes.
Risk assessment models like Value-at-Risk (VaR) quantify the maximum expected loss. These models are pivotal in finance for evaluating risk exposure.
Optimization Under Uncertainty
Stochastic optimization deals with systems affected by randomness. It optimizes decisions within uncertain contexts. This method balances risk against expected outcomes.
Sensitivity Analysis
Sensitivity analysis explores how output changes with different inputs. It determines the robustness of decisions against varying conditions.
Incorporating these principles and methodologies ensures a structured approach to probability analysis. Decision-makers gain a clear understanding of potential scenarios. They formulate strategies backed by rigorous statistical evidence. Such an approach equips them to make informed choices in the face of uncertainty.
How does the incorporation of probability analysis contribute to minimizing the risks and uncertainties in diverse business scenarios?
Probability Analysis in Business
In business, decision-makers face uncertainty. They rely on probability analysis. This tool quantifies the likelihood of outcomes. Understanding this aids in strategic planning.
Quantifying Risk
Businesses encounter various risks. These include financial, operational, and market risks. Probability analysis helps quantify these risks. It expresses potential outcomes numerically. Leaders can thus prioritize based on numbers.
Informed Decision-Making
Decisions rest on solid data foundations. Probability analysis provides such data. It informs business leaders. They base choices on likely outcomes. This reduces guesswork. Strategic decisions become more rational.
Risk Mitigation Strategies
Probability analysis pinpoints major risks. It helps develop mitigation strategies. Companies understand what to safeguard against. They allocate resources efficiently. This ensures a proactive approach.
Financial Planning
Sound financial planning is crucial. It relies heavily on accurate forecasts. Probability analysis improves these forecasts. It considers possible financial scenarios. Companies can then budget more effectively. They prepare for both best and worst-case scenarios.
Scenario Analysis
Diverse business scenarios exist. Probability analysis evaluates them. It helps compare risks across scenarios. This supports agile adaptation. Changes in the business landscape are less disruptive.
Optimizing Operations
Operational efficiency is key. Probability analysis aids in process optimization. It predicts the success of different operational models. Businesses streamline operations accordingly. They avoid pitfalls before they occur.
Pricing Strategies
Pricing is a complex issue. It determines competitiveness. Probability analysis assesses demand at various price points. Pricing strategies thus become more effective. They align with consumer behavior patterns.
Supply Chain Management
Supply chains can be volatile. Probability analysis aids in managing this volatility. It forecasts demand and supply fluctuations. Supply chain strategies adjust in response. This minimizes disruptions.
Portfolio Management
Investment decisions demand caution. Probability analysis helps assess asset risks. Portfolios balance risk and return better. They are tailored to meet investment goals.
Market Entry
Entering new markets is risky. Probability analysis evaluates market entry risks. It gauges success probabilities. Companies approach new ventures with numerical insight.
Crisis Management
Crisis management needs rapid response. Probability analysis foresees potential crises. Response strategies are then ready in advance. Companies tackle unexpected events with preparedness.
Competitive Advantage
Lasting competitive advantage matters. Probability analysis supports strategic positioning. It uncovers opportunities and threats. Companies gain a competitive edge. They stay ahead of market trends.
Conclusion
Probability analysis is pivotal. It turns uncertainty into manageable metrics. Businesses use it to limit potential losses. They make more confident, informed decisions. Their strategies are robust, adaptable. This minimizes risk across the board. Such is the power of incorporating probability in business.

Could you explain the role of probability distribution in predicting the potential outcomes and their likelihood in decision-making processes?
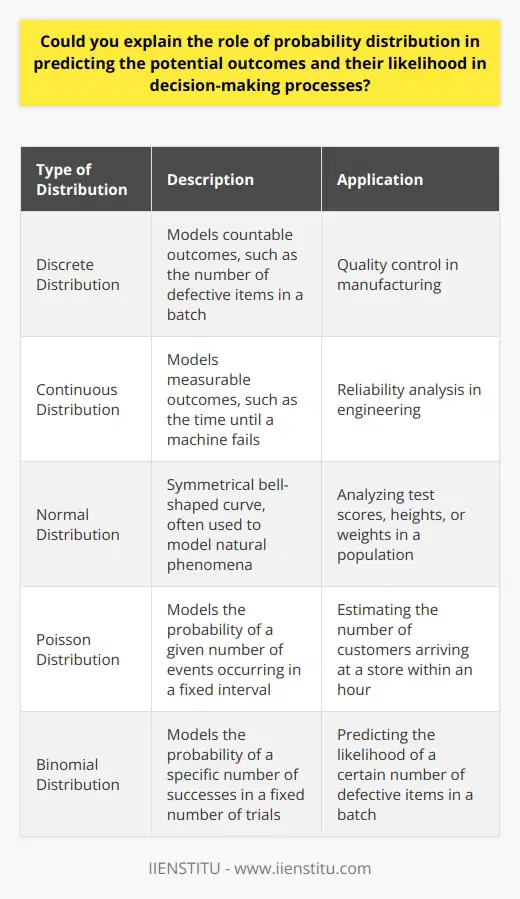
Understanding Probability Distributions
Probability distributions serve as a backbone in statistics. They model the potential outcomes of a random variable. Moreover, they assign probabilities to these outcomes.
Importance in Decision Making
During decision-making, leaders often face uncertainty. They analyze various outcomes and assess associated risks. Here, probability distributions come into play. They inform decision makers about the likelihood of different scenarios.
Probability distributions guide the choice between multiple options. They highlight the most probable outcomes. Additionally, they alert decision makers to the less likely ones.
Types of Distributions
There are different types of probability distributions.
- Discrete distributions relate to countable outcomes.
- Continuous distributions pertain to measurable outcomes.
Each type helps in predicting events relevant to its nature.
Predicting Outcomes
Decision makers rely on probability distributions to predict events.
Consider a simple coin toss.
- The coin has two possible outcomes.
- Each outcome has an equal probability of occurring.
This is the essence of a uniform distribution.
In more complex situations, distributions can be skewed. This means that outcomes may not have equal probabilities. Distributions can reveal this skewness.
Quantifying Risks
Probability distributions help in quantifying risks.
Lower probability events can carry higher risks.
Acknowledging this allows for better preparation. It also highlights the potential for higher rewards.
Application to Various Fields
Different fields use probability distributions to make informed decisions.
- Finance models stock market risks.
- Quality control predicts defects in manufacturing.
- Epidemiology estimates disease spread.
In each field, the correct use of distributions is crucial.
Conclusion
Probability distributions remain invaluable in decision-making. They encode the uncertainty inherent in any process. Moreover, they equip decision makers with quantifiable data. This enables well-informed and strategic thinking. Hence, they play a key role in predicting potential outcomes and their likelihoods.